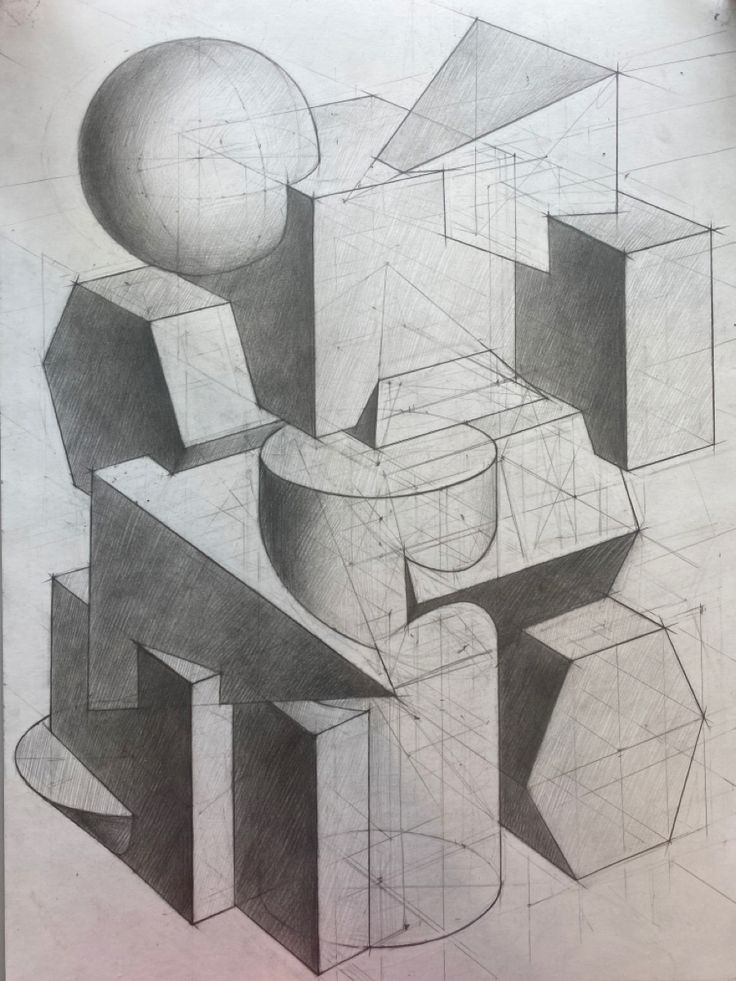
В математике Графом называется «система объектов произвольной природы (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов» [1].

Возможно для кого-то будет понятнее иная трактовка, когда Граф определяется как «математическая абстракция реальной системы любой природы, объекты которой обладают парными связями. Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин, и множества их парных связей, называемого множеством рёбер. Элемент множества рёбер есть пара элементов множества вершин» [2].

Исторически было замечено, что при решении сложных математических задач удобно изображать значимые данные объекты точками, а отношения между ними линиями, так это абстрактное представление данных и вошло в практику математики. Например, мы точно знаем, что первым в истории применением теории графов (но без использования термина «граф» и без рисования диаграмм графов) явилось решение Леонардом Эйлером в 1736-м году старинной народной задачи о семи Кёнигсбергских мостах. Головоломка ставила вопрос: как пройти по всем городским мостам так, чтобы маршрут не пролегал ни по одному из них дважды. Эйлер доказал, что это невозможно, представив мосты точками и обозначив их малыми буквами, отдельные области, на которые река разделяет сушу – заглавными, а переход моста — парой букв, обозначающих соединенные области суши.

Как рисовальщиков, нас в этой системе интересует подход и образ мыслей, который помогает обнаружить внутренние структурные взаимосвязи при изучении натуры и ее визуального представления в качестве опорных точек, ребер между ними и областей, разделенных этими ребрами.

Естественно, в искусстве эта модель прекрасно совпадает с пониманием основ аналитического моделирования объектов наблюдаемого мира и пространства между ними, особенно с алгоритмом Альберти-Чистякова рисования направлениями от точки до точки, где узловая точка – видимая вершина объекта или рельефа, направление от точки до точки – это ребро, а пространство между точками, ограниченное ребрами, – это плоскость. Каждая плоскость должна быть своего цвето-тона. Как только плоскость изменила положение по отношению к источнику освещения или к зрителю – должен измениться и тон, и цвет. Такой подход выражает скрытую морфологию изображения.

Вместе с тем, мы можем увидеть и явную морфологию, так называемую фактуру произведения если в нем явно сочетаются и плоскости, и по делу примененные линии, и где-то уместно сделанные точки. Изображение, в котором выявлены все морфологические элементы, выглядит богаче и полноценней.

Вместе с тем, чувствуется богатый потенциал применении этой системы для осмысления структурных взаимосвязей в композиции произведения, например, при искусствоведческом анализе композиции. Мы же знаем, что самые простые рекомендации в построении картины предлагают вписывать изобразительные элементы в простые геометрические фигуры. Эта тема не исследована и ждет «открытий чудных»

1. Теория графов: основные понятия и задачи. Графы как структура данных [Электронный ресурс] Точка доступа: https://function-x.ru/graphs1_relations.html (дата обращения 10.11.2020)
2. Граф (математика) [Электронный ресурс] Википедия. Точка доступа: https://Граф (математика) — Википедия (wikipedia.org) (дата обращения 15.12.2022)